Qué tan a menudo tirar los dados en Dungeons & Dragons
Nov 18, 2020
¿Qué tan a menudo en una sesión de D&D tiras dados? Hay gente que tira para todo y hay gente que preferiría nunca tirar. Pero ¿hay un número al qué apuntar de con qué frecuencia tirar?
Si pensamos que tirar un éxito como algo positivo para los PCs ¿Cuantas tiradas pueden esperar hacer antes de tener éxito? Si alguna vez has conocido a alguien a quien no le gusta tirar, porque podrían fallar ¿has considerado qué realmente deberían tirar más en vez de menos?
Hoy vamos a hablar de estadísticas, y dar muchas opiniones sobre cómo funciona tirar dados en Dungeons & Dragons.
Imagen de portada por Lucas Santos
Este post es una continuación de mi post anterior, en el que hablo de muchas de estas cosas desde una perspectiva más general, y comparo tirar dados en D&D contra PbtA, desde la perspectiva de las estadísticas.
¿Cual es la probabilidad de que tengas éxito en este check?
Esto es simple ¿cierto? tiras un d20 agregas tu bonus y lo comparas contra el DC de la tarea. Entonces, dado un DC 15 sin ningún bonus tu probabilidad de tener éxito es 6/20, es decir 30%. Y para el mismo DC 15 con un +5 Bonus la probabilidad de éxito es 11/20 = 55%.
En el primer caso esto es porque, de todos los números que un d20 puede generar, seis de ellos son iguales o mayores a 15
In the first case it’s becase, out of the numbers a d20 can generate, six are equal or greater than 15:
{1 , 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} están debajo de 15
{15, 16, 17, 18, 19, 20} son iguales o mayores a 15
Y para el segundo caso: d20 + 5
{6, 7, 8, 9, 10, 11, 12, 13, 14} estos nueve números están debajo de 15
{15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25} y estos once son iguales o mayores a 15
Utilizando la misma lógica podemos construir la siguiente tabla para Difficulty Class de 10 a 30 y Bonus de +0 a +10.
Probabilidad de éxito en un d20+Bonus contra un cierto DC
El 0% y 100% probablemente son obvios. Dado solo un +1 Bonus nunca puedes tirar un 25 y dado un +9 Bonus tienes garantizado tirar al menos un 20 incluso si el dado cae en uno.
Una nota rápida. D&D 5e no define fallos críticos en los libros. Entonces tirar un uno es mecánicamente insignificante más allá de haber tirado un uno. Adicionalmente solo define éxitos críticos durante combate, y estos resultan en tirar el doble de damage dice
Si dejamos del lado el concepto de “escalas de éxito” y pensamos en una tirada como éxito/fracaso entonces esto es un Ensallo de Bernoulli. De manera que podemos pensar en una tirada de dado similar a arrojar una moneda, en la que cada la do tiene probabilidades diferentes de caer, y cuyas caras son éxito & fracaso en vez de águila & sol.
Una probabilidad de 10% no es una probabilidad de 0%
Creo que esto es obvio cuando tiramos un solo d20, sabes que puedes tirar un 20 con un 5% de probabilidad. Pero conforme agregamos bonus y se mueven las probabilidades parece que este concepto se olvida. Contra un DC 10 incluso con un +7 Bonus la probabilidad de éxito es 90%, en otras palabras: tienes un 10% de probabilidad de fallar. En promedio, vas a fallar uno de cada diez intentos.
Esta es otra razón por la cual no hacer éxitos y fallos críticos. Siempre tener un 5% de probabildiad de fallo o 5% de probabilidad de éxito es inmensamente desbalanceado.
No se trata de si es qué vas a fallar. Se trata de cuando vas a fallar.
¿Cuándo vas a fallar?
Podemos extender el concepto de la Distribución de Bernoulli para contestar la siguiente pregunta: En promedio, ¿cuantos fracasos voy a observar antes de ver un éxito?
En otras palabras: (en promedio) ¿Cuantas veces voy a lanzar la moneda antes de ver la primera águila? o, para el interés de este post, ¿cuántas veces tengo que tirar un d20 antes de tener éxito en esta tarea, dado mi Bonus y el DC?
Ten en mente que siempre que hablamos de “antes” en este contexto, significa antes y hasta. Entonces si esperamos tirar tres veces antes de ver un éxito, entonces esperamos ver un éxito en tu tercera tirada en promedio
En probabilidad este número se describe por la Distribución geométrica. Y podemos pensar en este número como: el número de Ensayos de Bernoulli que necesitamos hacer para ver un éxito
Número esperado de tiradas antes de tener éxito para un d20+Bonus contra un cierto DC
Una vez más, los 1s y los vacíos deben ser claros. Dado un +9 bonus siempre vas a tener éxito contra un DC 10 incluso si tiras un 1 esto va a resultar en un total de 10. De modo que siempre toma una sola itarada pasar un DC 10 bajo estas condiciones. Para todo propósito un 1 en esta tabla es un éxito automático.
Por otro lado, los vacíos muestran que no hay ninguna oportunidad de tener éxito, sin importar cuantas veces se intente. Puedes seguir tirando ese d20 pero con un +0 bonus nunca vas a pasar un DC 21.
Antes de explicar el resto de la tabla, es importante considerar que estos valores son en promedio. Excepto por los 1s y las celdas vacías no hay ninguna certeza. Podrías tirar un d20 mil veces y no tirar un solo 20. Sería extremadamente extraño, pero es posible. Y is estas pensando en “desviación estándar” más adelante explico la desviación estándar de estos valores y por qué son importantes.
Las bandas de tiradas esperadas
Vamos a explicar por qué aparecen las bandas. Primero la banda 2. Siempre que tenemos un 50%, o más, de probabilidad de éxito, se espera que tires dos veces el dado antes de ver un éxito. Y tiene sentido. Si tienes un 80% de probabilidad de éxito es bastante probable que tengas éxito, pero siempre va a ser así; sin embargo es tan probable que la mayoría de las veces pasará al segundo intento.
Esta es la razón por la que fallar hacia adelante es importante. Si el DM mantiene el
DC 15y el PC tiene un+3 bonusla mayoría de las veces van a tener éxito a lo más en su tercer intento.
¿De dónde vienen estos números? El número esperado de Ensayos de Bernoulli requeridos antes de tener éxito se define como 1 ÷ la probabilidad de éxito
Entonces, si tu probabilidad de éxito es 50% se espera que hagas dos ensayos. Si es 75% se espera que hagas 1.333 ensayos. Pero, desde luego, hacer un tercio de ensayo no es posible; no puedes hacer un tercio de una tirada. De modo que redondeamos hacia arriba, como tienes que hacer un ensayo y un poco más, en realidad tienes que hacer dos ensayos.
Esta es la razón por la que la banda 2 es tan grande, siempre que tienes un 50% o más de probabilidad de éxito, esperamos que tires un éxito al segundo intento.
Es importante reiterar que esto no significa que sea más o menos probable tener éxito al primer intento; solo que la mayoría de las veces habrás tenido éxito al segundo intento.
Las bandas 3, 4, 5 y 7 tienen sentido intuitivo; conforme la probabilidad de éxito baja, entonces puedes esperar tener que intentarlo más veces antes de tener éxito. Sin embargo las bandas 10 y 20 me parecen saltos muy grandes.
Para entenderlo, consideremos que la banda 10 es el resultado de tener solo un 10% de probabilidad de éxito, lo cual significa que 💖✨EnPrOmEdIo✨💖 vas a tener éxito uno de cada diez intentos. En la banda 20 tienes un 5% de probabilidad de éxito, entonces vas a lograrlo una de cada veinte veces.
¿Y en realidad qué significa todo esto?
Como dije, refuerza la importancia de Fallar Hacia Adelante durante Skill Checks. Dado que, dependiendo del DC y Bonus, es probable que observes un éxito al segundo intento, entonces un solo fallo seguramente no debería tener impacto persistente en el juego, sin embargo, una serie de tiradas fallidas, si debería.
Segundo, pero más importante: ¡ahora sabemos cuantas tiradas debe hacer un jugador para tener éxito con su personaje!
Si estas frustrado porque tus jugadores, o por tu mismo, están tirando fallos, quizás no estas tirando suficientemente a menudo. La mayoría de las veces un PC necesita dos tiradas para tener éxito. Entonces, ese es el número mínimo de tiradas que un personaje debe hacer por sesión para sentir el éxito.
Esta es la razón por la que existe la ventaja. La mayoría de los checks van a tener éxito al segundo intento.
Finalmente. Si esperas que esta sesión sea difícil, o un PC no es particularmente bueno en este skill, entonces la sesión requiere más tiradas.
¿Qué es eso de la desviación estándar?
¡Si, la Desviación Estándar! definir la desviación estándar sin que tome una hora no es fácil. Entonces, voy a dar una definición que es útil durante el juego: 68% de los ensayos se van a comportar dentro del rango del promedio +/- una desviación estándar.
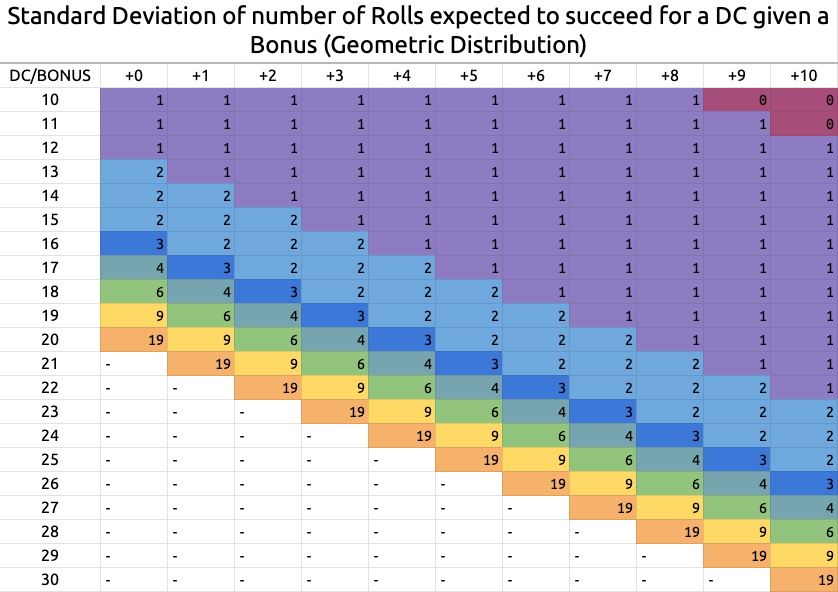La desviación estándar del número de tiradas que se espera tirar antes de tener éxito en un d20+Bonus contra cierta DC
Como he dicho: estos números son en promedio. Pero, como seguramente sabes, el promedio no es lo mismo que una experiencia específica. Sin embargo, de acuerdo a la definición anterior, 68% de las “series de tiradas” van a caer dentro de los rangos inferidos de esta tabla.
Por ejemplo, para un DC 15 y un +1 Bonus:
- En promedio se espera que tires tres veces antes de tener éxito. (ve la tabla de la sección anterior)
- Y el
68%de los ensayos habrás tenido éxito después de tirar entre una y cinco veces. Es decir[3-2, 3+2]dada la desviación estándar en esta tabla.
Desde luego, para un +10 Bonus y un DC 10 la desviación estándar es cero, porque siempre vas a tener éxito.
Entonces ¿qué tan a menudo deberías tiras dados por sesión? Bueno depende de los personajes y el Difficulty Class.
Por ejemplo: en combate, si un PC tiene un +4 Bonus contra un enemigo de AC 16 y si hacen entre 2 y 4 tiradas entonces habrán hecho un hit el 68% de las veces.
¿Es este un modo extraño y complejo de pensarlo? Si seguramente, pero si no le sacas ninguna otra cosa:
Tres veces. Todos deberían tirar los dados al menos tres veces por sesión.
Si te gustaría jugar con estas tablas las puedes encontrar aquí.
¡Gracias por leer este post! Ocasionalmente escribo sobre matemáticas en D&D, pero escribo regularmente sobre RPGs en general. Justo en este momento estoy escribiendo una aventura para 5e: Warlock Pixieland, inspirada por Cowboy Bebop! El anime clásico de los 90s.
Si te gustaría apoyarme puedes revisar Arcane Moon, mi aventura anterior disponible en DMs Guild, y puedes leer sobre el proceso de crearla aquí en mi blog.
También puedes encontrarme en twitter @darkade. Ahí puedes encontrar las noticias más recientes sobre lo que estoy trabajando. Dime si te gustaría leer más sobre dados, bonuses, y esta clase de cosas, porque todavía tengo muchas ideas al respecto distribución binomial ¿alguien?
Gracias por leer.
– Anya Reyes